Définitions

\(\triangleright\) Définition d'oscillateurs couplés

Des oscillateurs couplés sont des oscillateurs qui s'influencent l'un et l'autre.
Pour la suite, on considère des oscillateurs harmoniques et on négligera les frottements.

Mouvement

\(\triangleright\) Méthode d'étude du mouvement d'oscillateurs couplés

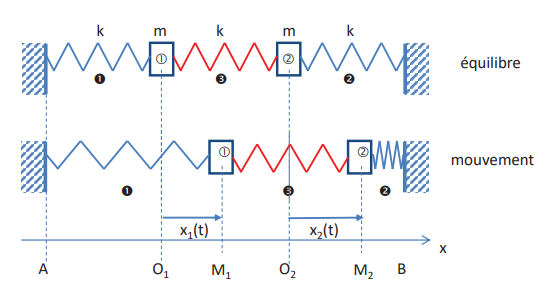
Pour trouver l'équation du mouvement d'oscillateurs couplés, on utilise le Deuxième loi de Newton - Principe fondamental de la dynamique avec un bilan des forces qui comptabilise les forces de la Loi de Hooke.
Attention, la variable de ces forces sera différente pour chaque ressorts.

Modes de vibration

\(\triangleright\) Modes propres d'oscillateurs couplés

On appelle modes propres les solutions de l'équation résultant du découplage lors la résolution de l'équation du mouvement.

\(\triangleright\) Généraltisation de la description du mouvement d'oscillateurs couplés

Tout mouvement d'oscillateurs couplés est la superposition de modes de vibrations.

Exemple

:
Etude du mouvement d'oscillateurs couplés:

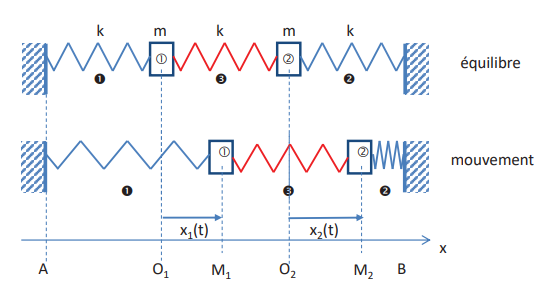
1
Grâce à la Loi de Hooke:
$$\vec F_1=-kx_1\vec i$$
$$\vec F_2=k(x_2-x_1)\vec i$$
$$\vec F_4=-kx_2\vec i$$
$$\vec F_3=-k(x_2-x_1)\vec i$$
2
On applique le Deuxième loi de Newton - Principe fondamental de la dynamique pour chaque mobile:
$$\begin{cases}m\ddot x_1=-kx_1+k(x_2-x_1)\\ m\ddot x_2=-kx_2-k(x_2-x_1)\end{cases}$$
$$\begin{cases}\ddot x_1=-2\omega_0^2x_1+\omega_0^2x_2\\ \ddot x_2=-2\omega_0^2x_2+\omega_0^2x_1\end{cases}$$
3
Principe de découplage
On cherche alors:
$$\begin{cases}x_1=aq_1(t)+cq_2(t)\\ x_2=bq_1(t)+dq_2(t)\end{cases}$$
Avec:
$$\begin{cases}q_1=A\cos(\omega_1t+\phi_1)\\ q_2=B\cos(\omega_2t+\phi_2)\end{cases}$$
Où \(q_1\) et \(q_2\) sont solutions de:
$$\begin{cases}\ddot q_1=-\omega_1q_1=\lambda_1q_1\\ \ddot q_2=-\omega_2q_2=\lambda_2q_2\end{cases}$$
4
Utilisation de la forme matricielle:
$$\vec {\ddot X}=M\vec{X}\qquad\text{avec } \vec X=\begin{pmatrix}x_1\\ x_2\end{pmatrix}\text{ et }M=\begin{pmatrix}-2\omega_0^2\qquad \omega_0^2\\ \omega_0^2\qquad -2\omega_0^2\end{pmatrix}$$
$$\vec {X}=P\vec{Y}\qquad\text{avec } \vec Y=\begin{pmatrix}q_1\\ q_2\end{pmatrix}\text{ et }P=\begin{pmatrix}a\qquad c\\ b\qquad d\end{pmatrix}$$
$$\vec {\ddot Y}=\lambda\Bbb I\vec{Y}\qquad\text{avec }\text{ et }M=\begin{pmatrix}\lambda_1\quad 0\\ 0\quad\lambda_2\end{pmatrix}$$
Avec: \(\lambda_1,\lambda_2\) les valeurs propres de la diagonalisation.
5
On peut alors écrire:
$$M\vec X=\ddot {\vec X}=\frac{\partial^2\vec X}{\partial t^2}\vec X=\frac{\partial^2 P\vec Y}{\partial t^2}=P\vec{\ddot Y}=P(\lambda\Bbb I\vec Y)=\lambda\Bbb I.P\vec Y=\lambda\Bbb I\vec X$$
Soit:
$$M\vec X=\lambda \Bbb I\vec X$$
6
On cherche alors les vecteurs propres associés aux valeurs propres \(\lambda\)
On diagonalise et on trouve:
$$\begin{cases}\omega_1=\omega_0\\ \omega_2=\sqrt 3\omega_0\end{cases}$$
$$\begin{pmatrix}a \\ b\end{pmatrix}=\begin{pmatrix}1\\ 1\end{pmatrix}$$
Et
$$\begin{pmatrix}c\\ d\end{pmatrix}=\begin{pmatrix}1\\ -1\end{pmatrix}$$
Finalement:
$$\begin{cases}x_1=q_1(t)+q_2(t)\\ x_2=q_1(t)-q_2(t)\end{cases}$$
Avec:
$$\begin{cases}q_1(t)=A\cos(\omega_0t+\phi_1)\\ q_2(t)=B\cos(\sqrt3\omega_0 t +\phi_2)\end{cases}$$